
Description
주어진 LinkedList에서 사이클이 시작되는 노드로 연결된 목록의 처음 index를 반환하는 문제입니다.
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
Example 1:
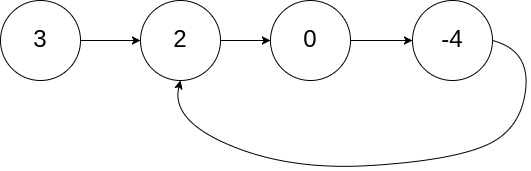
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
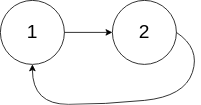
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.
Constraints:
- The number of the nodes in the list is in the range [0, 10^4].
- -10^5 <= Node.val <= 10^5
- pos is 1 or a valid index in the linked-list.
Follow up: Can you solve it using O(1) (i.e. constant) memory?
Solution 1. Set 사용
public ListNode detectCycle(ListNode head) {
// 1. using set
Set<ListNode> set = new HashSet<>();
while(head != null){
if(!set.add(head)){
return head;
}
head = head.next;
}
return null;
}
중복값을 저장하지 않는 Set를 이용하는 간단한 방법입니다. LinkedList를 순회하면서 set에 넣어주다가 이미 들어가 있는 ListNode를 add 할때의 head를 노드를 주면 됩니다. (put() > false반환). 순환이 끝날 때까지 중복되는 노드가 없다면 cycle이 없다는 의미므로 false를 반환합니다.
- 시간 복잡도 : O(N)
- 공간 복잡도 : O(N)
Solution 2. Floyd's cycle detection algorithm
public ListNode detectCycle(ListNode head) {
// 2. Two Pointers (Floyd's cycle detection algorithm)
ListNode slow = head;
ListNode fast = head;
while(fast != null && fast.next!=null){
slow = slow.next;
fast = fast.next.next;
if(slow == fast){ // 두 포인터가 만나는 지점까지 반복
slow = head; // slow head에서 다시 시작
while(slow != fast){ // 한칸씩 전진하며 두 포인터가 만날때 까지 다시 반복
slow = slow.next;
fast = fast.next;
}
return slow;
}
}
return null;
}
플로이드의 순환 탐색 알고리즘(Floyd's cycle detection algorithm)을 이용한 방법입니다.
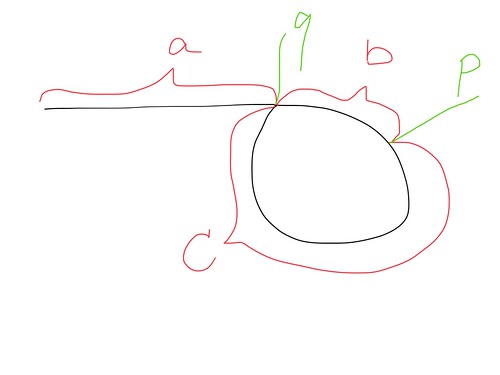
fast와 slow 포인터가 점 p에서 만날 때 그들이 달린 길이는 'a+2b+c'와 'a+b'이고 fast가 2배 빠르게 이동하기 때문에 a+2b+c == 2(a+b)가 됩니다. 최종적으로 우리는 'a==c'를 얻을 수 있습니다.
- slow포인터와 fast 포인터를 이동하면서 최초 만나는지점 p를 찾아냅니다.
- slow포인터를 head 로 위치시킵니다.
- slow포인터와 fast포인터를 동시에 한칸씩 전진하며 만나는지점 q를 찾아 반환합니다.
- 시간 복잡도 : O(N)
- 공간 복잡도 : O(1)
Reference
Linked List Cycle II - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
'알고리즘 > LeetCode' 카테고리의 다른 글
| [LeetCode] 167. Two Sum II - Input Array Is Sorted - 문제풀이 (0) | 2022.01.20 |
|---|---|
| [LeetCode] 283. Move Zeroes - 문제 풀이 (0) | 2022.01.20 |
| [LeetCode] 605. Can Place Flowers - 문제풀이 (0) | 2022.01.18 |
| [LeetCode] 88. Merge Sorted Array - 문제풀이 (0) | 2022.01.18 |
| [LeetCode] 1. Two Sum - 문제풀이 (0) | 2022.01.18 |
