
Description
주어진 트리가 root를 중심으로 거울에 비춘 것 처럼 대칭을 이루는지 여부, 즉 대칭 트리 여부를 반환하는 문제입니다.
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Example 1:
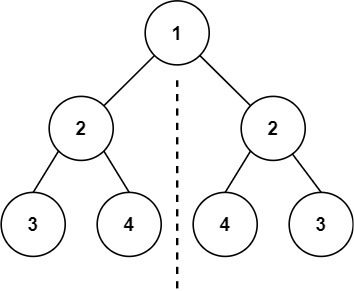
Input: root = [1,2,2,3,4,4,3]
Output: true
Example 2:
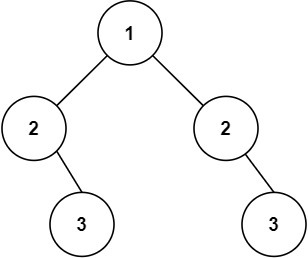
Input: root = [1,2,2,null,3,null,3]
Output: false
Constraints:
- The number of nodes in the tree is in the range [1, 1000].
- -100 <= Node.val <= 100
Follow up:
Could you solve it both recursively and iteratively?
Solution 1. DFS - 재귀호출(Recursion)
public boolean isSymmetric(TreeNode root) {
// 1. Recursion
if(root == null) return true;
return isSymmetric(root.left,root.right);
}
public boolean isSymmetric(TreeNode left, TreeNode right){
if(left == null && right == null) return true;
if(left == null || right == null) return false;
if(left.val != right.val){
return false;
}
return isSymmetric(left.left,right.right) && isSymmetric(left.right,right.left);
}
깊이우선탐색(DFS)알고리즘 처럼 재귀호출을 이용하여 대칭 여부를 판단해나갑니다. left의 left노드와 right의 right노드, 그리고 left.right와 right.left의 일치 여부를 비교해나가면 됩니다.
Solution 2. BFS - 반복(Iteration)
public boolean isSymmetri2(TreeNode root) {
// 2. Iteration
if(root == null) return true;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root.left);
q.offer(root.right);
while(!q.isEmpty()){
TreeNode left = q.poll();
TreeNode right = q.poll();
if(left == null && right != null) return false;
if(left != null && right == null) return false;
if(left != null && right != null){
if ( left.val != right.val){
return false;
}else{
q.offer(left.left);
q.offer(right.right);
q.offer(left.right);
q.offer(right.left);
}
}
}
return true;
}
BFS처럼 큐를 이용한 반복으로 두 노드의 대칭 여부를 판단해 나갑니다. 비교 대상 노드를 각각 순서대로 담은 뒤 비교해 나가고 모든 노드를 통과하여 큐가 비워졌을 경우 true를 반환해줍니다.
Reference
Symmetric Tree - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
'알고리즘 > LeetCode' 카테고리의 다른 글
| [LeetCode ] 112. Path Sum - 문제풀이 (0) | 2022.02.14 |
|---|---|
| [LeetCode] 226. Invert Binary Tree - 문제풀이 (0) | 2022.02.14 |
| [LeetCode] 78. Subsets - 문제풀이 (0) | 2022.02.13 |
| [Leetcode] 104. Maximum Depth of Binary Tree - 문제풀이 (0) | 2022.02.11 |
| [LeetCode] 560. Subarray Sum Equals K - 문제풀이 (0) | 2022.02.11 |
